How we use operations research to perfect healthcare rostering

Some clients have recently approached us asking this: “Sure, your algorithm auto-fills our staff shifts for us. But how does that work? Is it rule-based?”

We have never broken down the rationale in detail, so this is what we’re going to address today.

But first of all, is this Generative AI?

No. Generative AI (such as ChatGPT) is a poor approach for the scheduling problem, because it is notoriously bad with logic. It will not comply with your roster rules.

Operations Research: The Way Forward

The algorithm we use is actually based on Operations Research, a specific branch of mathematics.

It’s probably too abstract for someone without a solid mathematics background, but I intend to break it down for you. But before that, allow me to throw some formulas around (which we will explain in a second)

$\begin{align*} \text{Minimize} & \quad \sum\limits_{j=1}^{n} c_j x_j \\ \text{subject to: } & \quad \sum\limits_{j=1}^{n} a_ij x_j \leq b_i & \text{for}\quad i = 1,2,\dots,m \\ & \quad x_j \in Z \quad & \text{for} \quad j=1,2,\dots,p \quad(\leq n) \\ & \quad x_j \geq 0 \quad & \text{for} \quad j=p+1,\dots,n \end{align*}$

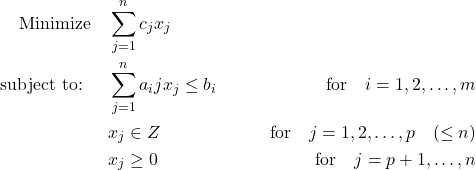
This is the most general description of a Mixed Integer Program (MIP) — It means a mathematical problem where we have certain variables and constraints. For a MIP problem, we force all the constraints and objective functions to be linear, and some of the variables are restricted to take integer values.

If you’re very savvy, you might notice that this is very similar — almost equal to the “linear programming” questions in HKDSE — because they are. This is just a more general, advanced formulation of those questions, but instead of 2 variables, x and y, now we deal with hundreds and thousands of variables, with some restricted to be integers.

If the formulation still doesn’t make full sense to you, you are not alone. Just follow along with us first.

Now, MIPs are not easy problems. In fact, most solvers out there cannot even guarantee an optimal solution for each MIP. There are MIPs with hundreds of thousands of variables that could be solved to optimality, while we’ve also seen MIPs with a few hundred parameters but hard to find a solution. And that makes MIPs an NP-hard problem (which is very difficult).

Along this mindset, it also follows that we can model a same problem with different techniques, and get very drastic performance and results depending on how we formulate it.

What does this have to do with rosters?

In principle, rosters are no different than mathematic problems: given a set of constraints, find an appropriate configuration of rosters to maximize fairness, staff satisfaction, etc.

So, whether a staff is on shift, on a particular day, for a particular shift, can actually be represented by a Boolean variable: true if staff is on shift, and false if not.

Rules such as “staff must take at most 1 shift every 3 days” can be formulated into constraints that limit the possibilities of the Boolean variables.

And the roster quality can be quantified into solid mathematical terms as well. For example, we want to minimize the imbalance of number of shifts by minimising the standard deviation of all shifts being taken by a staff.

Immediately you can see how flexible the algorithms can be: as long as we can describe the problem mathematically. For example, most rosters actually subdivide the fairness of shifts into shifts in “weekdays” and “weekends + public holidays”. It would indeed be advisable to make weekends fair for everyone. Another example is that you want to assign more senior staff to coach the most junior ones as much as possible (e.g. match professor with trainees).

Again, as long as we can express it mathematically, the degree of customisation is unlimited.

Using Operations Research in Action

Let’s demonstrate with a realistic scenario. Consider scheduling a 30-day roster in a hospital department with the following characteristics:

20 Nurses with varying skill levels (junior, intermediate, senior)
7-day scheduling period
3 shifts per day (Morning, Afternoon, Night)
Each shift requires 1 nurse
Nurses have different availabilities and preferences for shifts

We can formulate the problem as follows:

$\begin{falling}\text{Maximize} \quad & \sum\limits_{n=1}^N \sum\limits_{d=1}^D \sum\limits_{s=1}^S R_{n,d,s} x_{n,d,s} && \quad (1)\\ \text{Such That} \quad & \sum\limits_{n=1}^N x_{n,d,s} = 1 & \text{for} \quad s \in S, d \in D & \quad (2)\\ & \sum\limits_{s=1}^S x_{n,d,s} \leq 1 -L_{n,d} & \text{for} \quad n \in N, d\in D & \quad (3)\\ & x_{n,d,s} \in \{0, 1\} && \quad (4)\end{flalign}$

With the following parameters:

$\\ \text{N denotes the number of nurses. It is 20 in this case}\\\\ \text{D denotes the number of days to schedule for. It is 30 in this case.}\\\\ \text{S denotes the number of types of shift. }\\\text{It is 3 in this case (Morning, Afternoon, Night).}\\ \\x_{n,d,s} \text{ denotes whether a nurse is on shift on a particular }\\\text{day and shift type (e.g. 2024-09-12, Afternoon).}\\\text{If the person is on work, it is 1, else it is 0.}\\\\ R_{n,d,s} \text{ denotes if the nurse has a shift preference on a particular day}\\\text{and shift type. If there is a preference, it's 1, else it is 0.}\\\\ L_{n,d} \text{ denotes if the nurse is on leave that day. If so, it is 1, else it is 0. }$

Confused? Let us break it down one by one.

Bounds of the variable

You see that in (4), the variable x is confined to take values of either 0 or 1. This is what we want because a person is either on shift or not on shift for a particular day, and for a particular shift. This “binary” variable is the basis upon which we model our roster problem.

Each shift requries 1 nurse

This constraint is modelled in (2). If each shift requires one nurse, it means that adding up all the nurses shifts for a particular day and shift must equal 1.

No shift is assigned on leaves

This constraint is modelled in (3). If a person is on leave for a particular day, L_n,d would become 1, and hence the equation is forcing the person to take less than or equal to 0 shifts — practically forbidding them from taking a shift

Optimize by matching shift requests as much as possible

This is an objective, and it is modelled in (1). If a person requests, say, the shift on 12 September on Afternoon, R_n,(12 Sept),(afternoon) would be 1. And the mathematical model will try its best to find a solution that maximizes this term — which means that it will try and match your nurses’ shift requests with their assigned shifts.

In reality, we may have more complex rules (e.g. consider the skill mix and seniorities of nurses), which can also be modelled accordingly in such fashion. There are more specific rules, such as to forbid 2 people from scheduling together (usually to avoid having people of similar experience across different seniorities), or sometimes, some wards have a policy to force all day-offs to be more than 2 days in length. These would require more intricate modelling techniques, but they all are possible.

💡 If you want to learn more hands-on approach on how to formulate this in coding (especially Python), we actually have an e-book teaching you exactly that. Sign up for it here: https://8-hours.com.hk/e-book.

Solving MIP Problems: Branch and Cut

Now, formulating the problem is a challenge of it’s own, but the second challenge is much harder: how to generate a solution that actually maximizes the given term, and fulfills all the constraint. The algorithms are the core and heart of Operations Research, truly, and I’ll let you on one of the most robust algorithms we have: Branch and Cut Algorithm.

It starts off by ignoring the integrality constraints — aka, the variables x aren’t required to be 0 or 1.
It solves this relaxed problem using linear programming (LP) techniques (called Simplex Algorithm)
If the solution is entirely integer-valued, we’re done.
If not, the algorithm does 2 things:
1. Cutting Plane Generation: It tries to find valid inequalities (cuts) that are violated by the current fractional solution but satisfied by all integer solutions. These cuts tighten the LP relaxation, bringing it closer to the integer hull.
2. Branching: If cutting doesn’t yield an integer solution, it creates two new subproblems by choosing a variable with a fractional value and branching on it (e.g., nurse 1 is assigned 0.7 of a shift on Monday morning, so create one branch where this assignment is ≤ 0 and another where it’s ≥ 1).
Add the generated cuts to the model and re-optimize the linear program.
Repeat steps 4-5 for each subproblem created by branching.
Keep track of the best integer solution found so far (the uncumbent solution).
Prune branches that can’t possibly lead to a better solution than the current incumbent.
The process continues until all branches have been explored or pruned, guaranteeing that we find the optimal integer solution.

The key advantage of Branch and Cut over it’s predecessor Branch and Bound, is the addition of cutting planes. These cuts can significantly reduce the number of branches that needed to be explored, often leading to much faster solution times.

Sometimes, solvers do get stuck in either proving the solution they have is optimal, or they’re trying to find an even better solution, but in vain. However, in our experience, when the solver is looking so hard, it usually means that the current solution is already near-optimal, and represents a high-quality roster. In these cases, it is generally advisable to cut the solver early and retrieve the incumbent solution. (usually within 1 minute).

Advanced Techniques

While the basic formulation and algorithm are powerful, read-world scenarios often require more advanced techniques to handle larger problem sizes and additional complexities. For example:

Column Generation

This technique is particularly useful for problems with a large number of variables. Instead of considering all possible shift assignments at once, we start with a small subset and gradually introduce new variables (columns) that have the potential to improve the solution.

In healthcare rostering, this might involve starting with a basic set of shift patterns and gradually introducing more complex patterns as needed.

Decomposition Methods

Large rostering problems can often be decomposed into smaller, more manageable subproblems. For example, some wards schedule for different seniorities (e.g. 1st Call, 2nd Call, 3rd Call) separately, and a big ward problem is actually 3 subproblems for each call seniority.

Constraint Programming

This is a paradigm that’s particularly well-suited to problems with complex logical constraints. In healthcare rostering, it can be useful for handling rules like “if a nurse works a night shift, they must have the next day off.”

Meta-heuristics

While not guaranteed to find the optimal solution, meta-heuristics like Genetic Algorithms or Simulated Annealing can often find very good solutions quickly, even for extremely large problem instances.

Case Study: A Nursing Ward with Multiple Seniorities

Janice is an APN (advanced practice nurse) who came to us with her ward roster, which has the following rules: (for the sake of demonstration, we simplified some of the rules)

Every day, they need to assign 2 people to stand a night shift.
Every nurse should take at least 1 night per week.
There cannot be shifts assigned on leaves.
There are junior, senior nurses, and APN. Juniors cannot take the same shift with other juniors, and APNs cannot take the same shift with other APNs.
The roster should assign the number of shifts fairly.

We helped them formulate a model like this:

$\begin{align*} \text{Maximize} \quad & \frac{\sum\limits_{n=1}^{N} (c_n - m)^2}{N - 1} && \quad (1) \\ \text{Such That} \quad & \sum\limits_{n=1}^N x_{n,d,s} = 2 & \text{for} \quad s \in S, d \in D & \quad (2) \\ & \sum\limits_{d=\bar{d}}^{7} \sum\limits_{s=1}^{S} x_{n,\bar{d},s} \geq 1 & \text{for} \quad n \in N, \bar{d} \in [1, 2, \dots, D-6] & \quad (3) \\ & \sum\limits_{s=1}^S x_{n,d,s} \leq 1 -L_{n,d} & \text{for} \quad n \in N, d\in D & \quad (4) \\ & \sum\limits_{n=1}^{\bar{N}} x_{n,d,s} \leq 1 & \text{for} \quad s \in S, d \in D & \quad (5) \\ & \sum\limits_{n=1}^{\check{N}} x_{n,d,s} \leq 1 & \text{for} \quad s \in S, d \in D & \quad (6) \\ & c_n = \sum\limits_{d=1}^{D} \sum\limits_{s=1}^{S} x_{n,d,s} & \text{for} \quad n \in N & \quad (7) \\ & m_n = \sum\limits_{n=1}^{N} c_n && \quad (8) \\ & \\ & x_{n,d,s} \in \{0, 1\} && \quad \end{align*}$

$\\ \bar{N} \text{ indicates the number of APN.} \\ \check{N} \text{ indicates the number of juniors.}$

Constraints

(2) ensures that each shift is assigned to 2 nurses.

(3) ensures that every 7 days, there has to be at least 1 shift for each nurse.

(4) forces a person to not take any shifts if he/she is on a leave.

(5) and (6) forces at most 1 APN or 1 junior to take each shift, which prevents them from taking shifts together.

Objectives

(7) defines the shift counts for each person as c_n and (8) defines the mean shift count across all nurses.

The term (1), hence, describes the variance of shift counts, which is to be minimised in order to keep shift assignments as fair as possible for everyone.

Notably, this term is no longer linear — in fact it is convex quadratic, which would require a more advanced solver than MIP to solve. However, that is out of the scope of today.

Conclusion

Mathematical programming is an advanced way to automate roster scheduling, which carries the potential to significantly reduce scheduling time, saving precious time for medical staff to serve patients, or just take a good rest to charge up.

By leveraging the power of mathematical modelling, we can represent complex real world scheduling problems as structured sets of variables, constraints, and objectives. MIP then allows us to solve these problems efficiently, finding roster scheduling solutions that would be practically impossible to discover through manual methods.

In the end, while the mathematics behind these systems may be complex, their impact is simple and profound: better schedules, happier staff, and improved patient care. And that’s a formula for success in any healthcare setting.

Optimize Your Ward Scheduling with Expert Assistance

Our Scheduling Service

If you’re looking to implement an efficient, fair, and compliant ward roster scheduling system, we can help. We offer personalized algorithm development and web-based solutions tailored to your specific needs. Learn more about how we can transform your scheduling process at https://8-hours.com.hk.

Learn to Schedule with Program

If you want to try make your own rostering algorithm, you can learn it with our free e-book, “Programmatic Roster Scheduling”. This guide introduces you to the basics of using programming to create efficient and fair schedules. You will learn how to translate ward rules into code, automate repetitive tasks, and generate optimized rosters with ease. Because most doctors have little programming experience, I’ve written it for beginners in Python. Download it for free at https://8-hours.com.hk/e-book and start learning now!